1457. 二叉树中的伪回文路径 Medium
给你一棵二叉树,每个节点的值为 1 到 9 。我们称二叉树中的一条路径是 「伪回文」的,当它满足:路径经过的所有节点值的排列中,存在一个回文序列。
请你返回从根到叶子节点的所有路径中 伪回文 路径的数目。
示例 1:
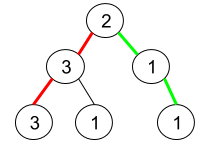
输入:root = [2,3,1,3,1,null,1]
输出:2
解释:上图为给定的二叉树。总共有 3 条从根到叶子的路径:红色路径 [2,3,3] ,绿色路径 [2,1,1] 和路径 [2,3,1] 。
在这些路径中,只有红色和绿色的路径是伪回文路径,因为红色路径 [2,3,3] 存在回文排列 [3,2,3] ,绿色路径 [2,1,1] 存在回文排列 [1,2,1] 。
示例 2:
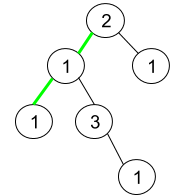
输入:root = [2,1,1,1,3,null,null,null,null,null,1]
输出:1
解释:上图为给定二叉树。总共有 3 条从根到叶子的路径:绿色路径 [2,1,1] ,路径 [2,1,3,1] 和路径 [2,1] 。
这些路径中只有绿色路径是伪回文路径,因为 [2,1,1] 存在回文排列 [1,2,1] 。
示例 3:
输入:root = [9]
输出:1
解题思路
输入: 一个二叉树的根节点 root,里面的值都是 1 - 9。
输出: 返回这棵树的 “伪回文” 路径的数目。
本题属于自顶向下 DFS问题。
这道题的关键在于要判断 “伪回文”,要想满足回文路径就需要保证集合里的值最多只能有一个是奇数个
我们可以 自顶向下 遍历二叉树记录路径,可以用数组也可以用 set
这里可以用 set 来判断当前值是否已经出现过一次,如果出现过则移除,如果没有在 set 中则添加进去
当访问到叶子节点时判断 len(set) <= 1 ,满足条件就是伪回文路径并返回 1,否则返回 0
代码实现
class Solution:
def pseudoPalindromicPaths(self, root: Optional[TreeNode]) -> int:
def dfs(node, odd_set):
if not node:
return 0
# 如果当前节点值已经在集合中,说明已经出现过一次(变为偶数次),移除
# 否则添加进集合,代表奇数次
if node.val in odd_set:
odd_set.remove(node.val)
else:
odd_set.add(node.val)
# 如果是叶子节点
if not node.left and not node.right:
# 伪回文条件:最多只有一个数字出现了奇数次
return 1 if len(odd_set) <= 1 else 0
# 注意:为了避免 left 和 right 共用同一个集合,必须创建副本
left_count = dfs(node.left, set(odd_set))
right_count = dfs(node.right, set(odd_set))
return left_count + right_count
# 初始传入空集合,代表当前路径上没有数字
return dfs(root, set())/**
* @param {TreeNode} root
* @return {number}
*/
var pseudoPalindromicPaths = function(root) {
function dfs(node, oddSet) {
if (!node) return 0;
if (oddSet.has(node.val)) {
oddSet.delete(node.val);
} else {
oddSet.add(node.val);
}
if (!node.left && !node.right) {
return oddSet.size <= 1 ? 1 : 0;
}
const left = dfs(node.left, new Set(oddSet));
const right = dfs(node.right, new Set(oddSet));
return left + right;
}
return dfs(root, new Set());
};复杂度分析
时间复杂度:O(n)
空间复杂度:O(h),h 为树的高度