865. 具有所有最深节点的最小子树 Medium
给定一个根为 root 的二叉树,每个节点的深度是 该节点到根的最短距离 。
返回包含原始树中所有 最深节点 的 最小子树 。
如果一个节点在 整个树 的任意节点之间具有最大的深度,则该节点是 最深的 。
一个节点的 子树 是该节点加上它的所有后代的集合。
示例 1:
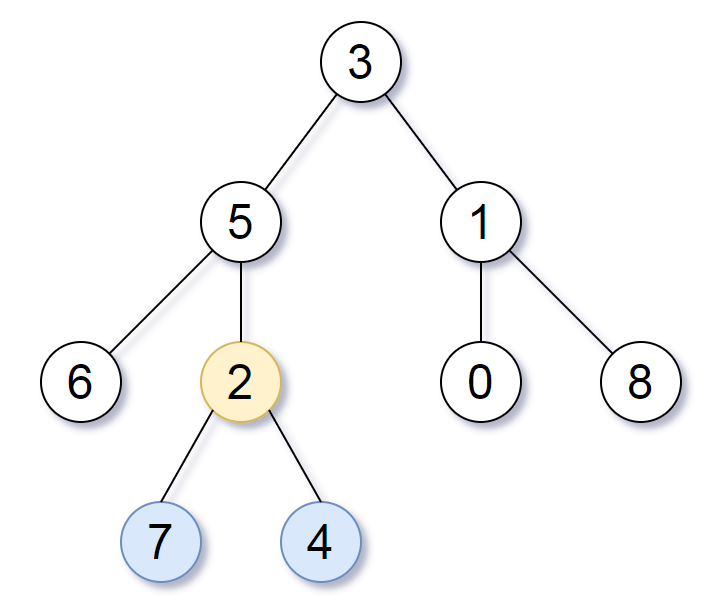
输入:root = [3,5,1,6,2,0,8,null,null,7,4]
输出:[2,7,4]
解释:
我们返回值为 2 的节点,在图中用黄色标记。
在图中用蓝色标记的是树的最深的节点。
注意,节点 5、3 和 2 包含树中最深的节点,但节点 2 的子树最小,因此我们返回它。
示例 2:
输入:root = [1]
输出:[1]
解释:根节点是树中最深的节点。
示例 3:
输入:root = [0,1,3,null,2]
输出:[2]
解释:树中最深的节点为 2 ,有效子树为节点 2、1 和 0 的子树,但节点 2 的子树最小。
解题思路
输入: 一个二叉树的根节点 root。
输出: 返回包含所有最深节点的最小公共祖先
本题可以用 自顶向下 DFS 也可以用 自底向上 解决。
自顶向下 DFS
我们可以维护两个全局变量 ans max_depth 记录答案和最大深度
- 我们向下遍历时可以将下一层深度传入,并在递归求最大深度的过程中每次都更新最大深度值
- 当判断左右子树相等并都到达最大深度的时候就是答案
- 由于最大深度只会不断递增,所以最终全部遍历过后一定可以得到整棵树的最大深度值
自底向上 DFS
我们可以将每颗子树都看成一个子问题,我们只需要知道:
- 这颗子树的最深叶子深度
- 这颗子树的最深叶子节点的公共祖先
分类讨论:
- 设子树的根节点为
node,node的左子树的高度为leftHeight,node的右子树的高度为rightHeight。 - 如果
leftHeight > rightHeight,那么子树的高度为leftHeight + 1,lca 是左子树的 lca。 - 如果
leftHeight < rightHeight,那么子树的高度为rightHeight + 1,lca 是右子树的 lca。 - 如果
leftHeight = rightHeight,那么子树的高度为leftHeight + 1,lca 就是 node。反证法:如果 lca 在左子树中,那么 lca 不是右子树的最深叶结点的祖先,这不对;如果 lca 在右子树中,那么 lca 不是左子树的最深叶结点的祖先,这也不对;如果 lca 在 node 的上面,那就不符合「最近」的要求。所以 lca 只能是 node。
代码实现
自顶向下 DFS
python
class Solution:
def subtreeWithAllDeepest(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
# 记录最深的深度
max_depth = 0
# 最小公共子树根节点
ans = None
def dfs(node, depth):
nonlocal max_depth, ans
if not node:
# 更新全局最大深度
max_depth = max(max_depth, depth)
return depth # 空节点返回当前深度用于比较
# 分别计算左右子树的最大深度
left = dfs(node.left, depth + 1)
right = dfs(node.right, depth + 1)
# 如果当前节点的左右子树都达到了最大深度
if left == right == max_depth:
ans = node # 当前节点即为包含所有最深节点的最小子树根
# 返回左右子树中更深的一边
return max(left, right)
dfs(root, 0)
return ansjavascript
/**
* @param {TreeNode} root
* @return {TreeNode}
*/
var subtreeWithAllDeepest = function(root) {
let ans = null;
let maxDepth = 0;
function dfs(node, depth) {
if (!node) {
maxDepth = Math.max(maxDepth, depth);
return depth;
}
const left = dfs(node.left, depth + 1);
const right = dfs(node.right, depth + 1);
if (left == right && left == maxDepth)
ans = node
return Math.max(left, right);
}
dfs(root, 0);
return ans;
};自底向上 DFS
python
class Solution:
def subtreeWithAllDeepest(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
# 自底向上 DFS
# 定义一个自底向上的 DFS 函数,返回 (子树最大深度, 最深节点的最近公共祖先)
def dfs(node):
if not node:
# 空节点深度为 0,没有祖先
return 0, None
# 递归左右子树,获取它们的最大深度和对应的最小公共祖先
left_depth, left_lca = dfs(node.left)
right_depth, right_lca = dfs(node.right)
# 根据左右子树的深度判断:
if left_depth > right_depth:
# 左子树更深,返回左子树的信息,深度 +1
return left_depth + 1, left_lca
elif right_depth > left_depth:
# 右子树更深,返回右子树的信息,深度 +1
return right_depth + 1, right_lca
else:
# 左右深度相等,当前节点是最深节点的公共祖先
return left_depth + 1, node
# 返回最终的最近公共祖先节点
return dfs(root)[1]javascript
/**
* @param {TreeNode} root
* @return {TreeNode}
*/
var subtreeWithAllDeepest = function(root) {
// 自底向上 DFS
function dfs(node) {
if (!node) return [0, null];
const [leftDepth, leftLca] = dfs(node.left);
const [rightDepth, rightLca] = dfs(node.right);
if (leftDepth < rightDepth)
return [rightDepth + 1, rightLca];
if (leftDepth > rightDepth)
return [leftDepth + 1, leftLca];
return [leftDepth + 1, node];
}
return dfs(root)[1];
}复杂度分析
时间复杂度:O(n)
空间复杂度:O(n)