538. 把二叉搜索树转换为累加树 Medium
给出二叉 搜索 树的根节点,该树的节点值各不相同,请你将其转换为累加树(Greater Sum Tree),使每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。
提醒一下,二叉搜索树满足下列约束条件:
- 节点的左子树仅包含键 小于 节点键的节点。
- 节点的右子树仅包含键 大于 节点键的节点。
- 左右子树也必须是二叉搜索树。
注意:本题和 1038 相同
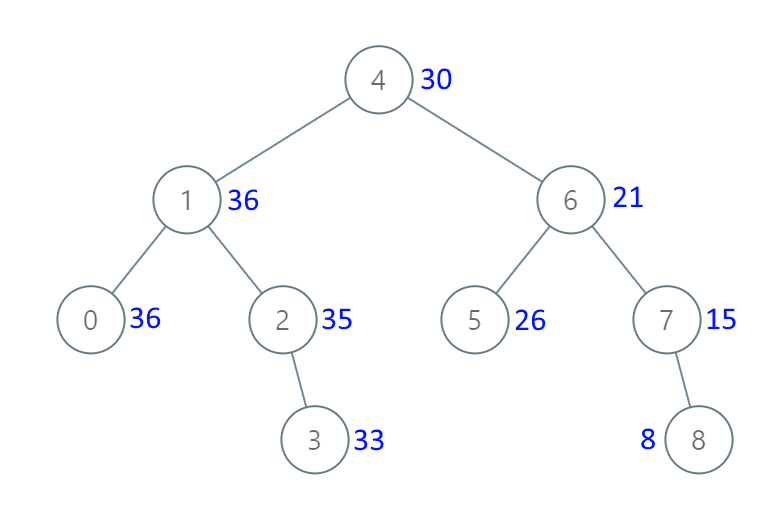
示例 1:
输入:[4,1,6,0,2,5,7,null,null,null,3,null,null,null,8]
输出:[30,36,21,36,35,26,15,null,null,null,33,null,null,null,8]
示例 2:
输入:root = [0,null,1]
输出:[1,null,1]
示例 3:
输入:root = [1,0,2]
输出:[3,3,2]
示例 4:
输入:root = [3,2,4,1]
输出:[7,9,4,10]
解题思路
输入:二叉搜索树的根节点 root
输出:将其转化成累加树并返回
这道题是属于 二叉搜索树 + 反中序遍历 问题。
二叉搜索树(BST)特性:右子树的值 > 当前节点值 > 左子树的值。
所以关键点在于要从最大值开始累加,也就是最右边的值开始,因此要从右到左遍历,也就是 反中序遍历 (右 -> 中 -> 左)。
因为要不断累加需要记录上一次的值,所以我们可以用一个全局变量 total 记录
我们先通过 dfs(node.right) 遍历到达最大值节点,也就是在 “归” 的时候开始不断累加 total += node.val 就是当前节点的累加值
然后再递归 dfs(node.left) 可以再遍历的过程中就直接累加,也就是在 “递” 的时候就不断累加 total += node.val,就是当前节点的累加值
最后直接返回根节点就是答案,所以也算是一种 有递有归 的类型题。
代码实现
class Solution:
def convertBST(self, root: Optional[TreeNode]) -> Optional[TreeNode]:
total = 0 # 初始化全局变量,记录已访问节点值的累加和
def dfs(node):
nonlocal total # 使用外部的 total 变量,允许在递归中修改
if not node:
return # 空节点直接返回,无需处理
# 先递归访问右子树(右子树节点值较大,确保先处理更大的值)
dfs(node.right)
# 处理当前节点:将当前节点值累加到 total,并更新节点值为累加和
total += node.val # 累加当前节点值到 total(包含当前节点值)
node.val = total # 更新节点值为 total(大于或等于当前节点值的和)
# 再递归访问左子树(左子树节点值较小,继续累加)
dfs(node.left)
dfs(root) # 从根节点开始处理整棵树
return root # 返回转换后的累加树根节点/**
* @param {TreeNode} root
* @return {TreeNode}
*/
var convertBST = function(root) {
let total = 0;
function dfs(node) {
if (!node) return;
dfs(node.right);
total += node.val;
node.val = total;
dfs(node.left);
}
dfs(root);
return root;
};复杂度分析
时间复杂度:O(n)
空间复杂度:O(n)