104. 二叉树的最大深度 Easy

给定一个二叉树 root ，返回其最大深度。

二叉树的 最大深度 是指从根节点到最远叶子节点的最长路径上的节点数。

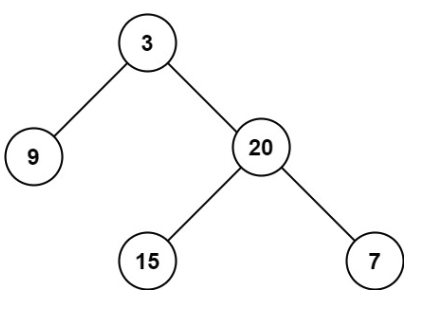
示例 1:
输入：root = [3,9,20,null,null,15,7]
输出：3

示例 2:
输入：root = [1,null,2]
输出：2

解题思路

输入： 一个二叉树的根节点 root。

输出： 返回最大深度

本题可以用自底向上 DFS（后序遍历） 也可以用 自顶向下 DFS 解决。

我们使用递归来计算每个节点的最大深度，其核心逻辑是：

• 对于每个节点，它的最大深度 = max(左子树深度, 右子树深度) + 1
• 空节点返回深度 0（递归终止条件）
• 从叶子节点开始逐层向上返回深度，最终在根节点返回整棵树的最大深度

这是一种 后序遍历 （left → right → root） 的过程，递归地先处理子树，再汇总结果，最终得到整棵树的最大深度。

代码实现

自底向上 DFS

python

class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        # 如果当前节点为空，说明这是一棵空树，深度为 0
        if not root:
            return 0

        # 否则，递归计算左右子树的最大深度，并取其中较大值加 1（当前节点本身）
        return 1 + max(self.maxDepth(root.left), self.maxDepth(root.right))

javascript

const maxDepth = function(root) {
    // 如果当前节点为空，说明这是一棵空树，深度为 0
    if (!root) return 0;

    // 否则，递归计算左右子树的最大深度，并取其中较大值加 1（当前节点本身）
    return Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
};

自顶向下 DFS

python

class Solution:
    def maxDepth(self, root: Optional[TreeNode]) -> int:
        def dfs(node, depth):
            if not node:
                return depth
            
            left = dfs(node.left, depth + 1)
            right = dfs(node.right, depth + 1)

            return max(left, right)
        return dfs(root, 0)

javascript

const maxDepth = function(root) {
    function dfs(node, depth) {
        if (!node) return depth;

        const left = dfs(node.left, depth + 1);
        const right = dfs(node.right, depth + 1);

        return Math.max(left, right);
    }

    return dfs(root, 0);
};

复杂度分析

时间复杂度：O(n)

空间复杂度：O(h)

链接

104 国际版

104 中文版