257. 二叉树的所有路径 Easy
给你一个二叉树的根节点 root ,按 任意顺序 ,返回所有从根节点到叶子节点的路径。
叶子节点 是指没有子节点的节点。
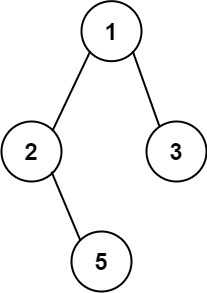
示例 1:
输入:root = [1,2,3,null,5]
输出:["1->2->5","1->3"]
示例 2:
输入:root = [1]
输出:["1"]
解题思路
输入: 一个二叉树的根节点 root。
输出: 返回任意顺序的从根节点到叶子结点的路径。
本题属于深度优先遍历(DFS)+ 路径记录 + 回溯问题。
方法一:递归 DFS + 回溯
利用 DFS 的特点,在递归过程中用一个数组 path 实时记录当前路径。
- 每访问一个节点,就将该节点加入路径;
- 若当前节点是叶子节点,则将 path 拼接成字符串后加入结果集;
- 遍历完当前节点的左右子树后,使用 path.pop() 回溯,撤销当前选择;
- 按顺序递归左子树和右子树,最终得到所有从根到叶子的路径。
方法二:迭代 DFS(用栈模拟递归)
我们可以使用栈来模拟 DFS 过程,避免递归调用。
- 初始化栈,元素为 (当前节点, 当前路径字符串) 的元组;
- 每次从栈中弹出一个节点及其路径:
- 如果是叶子节点,则将路径加入结果集;
- 否则将其右子节点和左子节点依次压入栈,并拼接好路径字符串;
- 由于栈是先进后出结构,为了保持“先左后右”的遍历顺序,右子节点先入栈,左子节点后入栈。
代码实现
python
class Solution:
def binaryTreePaths(self, root: Optional[TreeNode]) -> List[str]:
# ============ 循环写法 ================ #
if not root:
return []
res = [] # 存储所有路径结果
stack = [(root, str(root.val))] # 初始栈:节点 + 当前路径字符串
while stack:
node, path = stack.pop()
# 如果是叶子节点,加入结果列表
if not node.left and not node.right:
res.append(path)
# 注意:先压右子树,再压左子树,这样左子树会先处理(模拟递归顺序)
if node.right:
stack.append((node.right, path + '->' + str(node.right.val)))
if node.left:
stack.append((node.left, path + '->' + str(node.left.val)))
return res
# ============ 递归写法 ================ #
ans = [] # 用于存储所有路径结果
path = [] # 临时路径记录
def dfs(node):
if not node:
return # 遇到空节点直接返回
# 将当前节点值加入路径(转为字符串)
path.append(str(node.val))
# 如果是叶子节点,构造路径字符串并加入结果
if not node.left and not node.right:
ans.append('->'.join(path))
# 继续递归遍历左右子树
dfs(node.left)
dfs(node.right)
# 回溯:撤销本次递归对路径的修改
path.pop()
# 从根节点开始 DFS
dfs(root)
return ansjavascript
// ======= 循环写法 =====
// 存储所有路径结果
const ans = [];
// 初始栈:节点 + 当前路径字符串
const stack = [[root, String(root.val)]];
while (stack.length) {
const [node, path] = stack.pop();
// 如果是叶子节点,加入结果列表
if (!node.left && !node.right)
ans.push(path);
// 注意:先压右子树,再压左子树,这样左子树会先处理(模拟递归顺序)
if (node.right)
stack.push([node.right, path + '->' + String(node.right.val)]);
if (node.left)
stack.push([node.left, path + '->' + String(node.left.val)])
}
return ans;
// ======= 递归写法 =======
// 用于存储所有路径结果
const ans = [];
// 临时路径记录
const path = [];
function dfs(node) {
// 遇到空节点直接返回
if (!node) return;
// 将当前节点值加入路径
path.push(node.val);
// 如果是叶子节点,构造路径字符串并加入结果
if (!node.left && !node.right)
ans.push(path.join('->'));
// 继续递归遍历左右子树
dfs(node.left)
dfs(node.right)
// 回溯:撤销本次递归对路径的修改
path.pop();
}
// 从根节点开始 DFS
dfs(root)
return ans;复杂度分析
时间复杂度:O(n)
空间复杂度:O(n)