2090. 半径为 k 的子数组平均值 Medium
给你一个下标从 0 开始的数组 nums ,数组中有 n 个整数,另给你一个整数 k 。
半径为 k 的子数组平均值 是指:nums 中一个以下标 i 为 中心 且 半径 为 k 的子数组中所有元素的平均值,即下标在 i - k 和 i + k 范围(含 i - k 和 i + k)内所有元素的平均值。如果在下标 i 前或后不足 k 个元素,那么 半径为 k 的子数组平均值 是 -1 。
构建并返回一个长度为 n 的数组 avgs ,其中 avgs[i] 是以下标 i 为中心的子数组的 半径为 k 的子数组平均值 。
x 个元素的 平均值 是 x 个元素相加之和除以 x ,此时使用截断式 整数除法 ,即需要去掉结果的小数部分。
例如,四个元素 2、3、1 和 5 的平均值是 (2 + 3 + 1 + 5) / 4 = 11 / 4 = 2.75,截断后得到 2 。
示例 1:
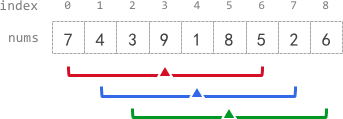
输入:nums = [7,4,3,9,1,8,5,2,6], k = 3 输出:[-1,-1,-1,5,4,4,-1,-1,-1]
解释:
avg[0]、avg[1] 和 avg[2] 是 -1 ,因为在这几个下标前的元素数量都不足 k 个。
中心为下标 3 且半径为 3 的子数组的元素总和是:7 + 4 + 3 + 9 + 1 + 8 + 5 = 37 。使用截断式 整数除法,avg[3] = 37 / 7 = 5 。
中心为下标 4 的子数组,avg[4] = (4 + 3 + 9 + 1 + 8 + 5 + 2) / 7 = 4 。
中心为下标 5 的子数组,avg[5] = (3 + 9 + 1 + 8 + 5 + 2 + 6) / 7 = 4 。
avg[6]、avg[7] 和 avg[8] 是 -1 ,因为在这几个下标后的元素数量都不足 k 个 。
示例 2:
输入:nums = [100000], k = 0
输出:[100000]
解释:
中心为下标 0 且半径 0 的子数组的元素总和是:100000 。avg[0] = 100000 / 1 = 100000 。
示例 3:
输入:nums = [8], k = 100000
输出:[-1]
解释:
avg[0] 是 -1 ,因为在下标 0 前后的元素数量均不足 k 。
解题思路
输入:一个整数数组 nums 和一个整数 k
输出:返回以下标 i 为 中心 且 半径 为 k 的子数组中所有元素的平均值
本题属于 固定长度滑动窗口类型 类型。
- 窗口的长度为
2 * k + 1 - 当窗口长度为 0 时直接返回原数组
- 当窗口长度大于数组长度时,返回
[-1] * len(nums) - 我们只需要在
[k, n - k]中计算平均值即可
代码实现
from typing import List
class Solution:
def getAverages(self, nums: List[int], k: int) -> List[int]:
# 初始化结果数组,全部填充 -1
n = len(nums)
result = [-1] * n
# 如果 k=0,每个位置的平均值就是自身
if k == 0:
return nums
# 子数组长度为 2k+1
window_size = 2 * k + 1
# 如果窗口大小大于数组长度,所有位置都返回 -1
if window_size > n:
return result
# 计算第一个窗口的和(索引 k 对应的子数组 nums[0:2k+1])
window_sum = sum(nums[:window_size])
# 计算第一个有效位置(索引 k)的平均值
result[k] = window_sum // window_size
# 滑动窗口,计算后续位置的平均值
for i in range(k + 1, n - k):
# 减去窗口左侧元素,加入右侧新元素
window_sum = window_sum - nums[i - k - 1] + nums[i + k]
result[i] = window_sum // window_size
return result/**
* @param {number[]} nums
* @param {number} k
* @return {number[]}
*/
var getAverages = function(nums, k) {
if (k == 0) return nums;
const windowSize = 2 * k + 1;
const ans = new Array(nums.length).fill(-1);
if (windowSize > nums.length) {
return ans;
}
let windowSum = 0;
for (let i = 0; i < windowSize; i++) {
windowSum += nums[i];
}
ans[k] = Math.floor(windowSum / windowSize);
for (let i = k + 1; i < nums.length - k; i++) {
windowSum = windowSum - nums[i - k - 1] + nums[i + k];
ans[i] = Math.floor(windowSum / windowSize);
}
return ans;
};复杂度分析
时间复杂度:O(n)
空间复杂度:O(n)