1161. 最大层内元素和 Medium
给你一个二叉树的根节点 root。设根节点位于二叉树的第 1 层,而根节点的子节点位于第 2 层,依此类推。
请返回层内元素之和 最大 的那几层(可能只有一层)的层号,并返回其中 最小 的那个。
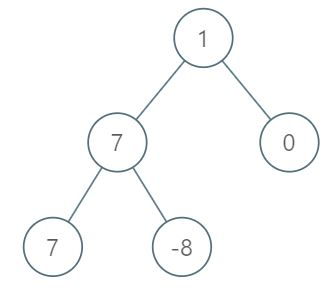
示例 1:
输入:root = [1,7,0,7,-8,null,null]
输出:2
解释:
第 1 层各元素之和为 1,
第 2 层各元素之和为 7 + 0 = 7,
第 3 层各元素之和为 7 + -8 = -1,
所以我们返回第 2 层的层号,它的层内元素之和最大。
示例 2:
输入:root = [989,null,10250,98693,-89388,null,null,null,-32127]
输出:2
解题思路
输入: 一个二叉树的根节点 root
输出: 返回层内元素之和最大的层号,如果有多个最大值则返回最小的层号
本题属于BFS遍历问题。
- 用队列做层序遍历;
level记录当前层号,从 1 开始;- 对当前层的所有节点求和,与历史最大值比较并更新答案层号;
- 返回最大和对应的最小层号(天然满足,因为我们从上到下遍历)。
代码实现
python
class Solution:
def maxLevelSum(self, root: Optional[TreeNode]) -> int:
queue = [root] # 初始化队列,将根节点放入队列
max_level = 1 # 记录最大节点和的层数,初始为第1层
max_sum = float('-inf') # 记录当前最大的层节点和,初始为负无穷
level = 1 # 当前层的层数,初始为1
while queue:
level_sum = 0 # 当前层的节点值和
next_level = [] # 存储下一层的节点
# 遍历当前层的所有节点
for node in queue:
level_sum += node.val # 计算当前层的节点值和
# 如果有左子节点,将其加入下一层队列
if node.left:
next_level.append(node.left)
# 如果有右子节点,将其加入下一层队列
if node.right:
next_level.append(node.right)
# 如果当前层的节点值和大于目前的最大节点和,更新最大值和层数
if level_sum > max_sum:
max_sum = level_sum
max_level = level
# 更新队列为下一层的节点,层数加1
queue = next_level
level += 1
return max_level # 返回最大节点和所在的层数javascript
var maxLevelSum = function(root) {
let queue = [root];
let level = 1;
let maxLevel = 1
let maxSum = -Infinity;
while (queue.length) {
let levelSum = 0;
const nextLevel = [];
const size = queue.length;
for (let i = 0; i < size; i++) {
const node = queue[i];
levelSum += node.val;
if (node.left) nextLevel.push(node.left);
if (node.right) nextLevel.push(node.right);
}
if (levelSum > maxSum) {
maxSum = levelSum;
maxLevel = level;
}
level++;
queue = nextLevel;
}
return maxLevel;
};复杂度分析
时间复杂度:O(n)
空间复杂度:O(w) (BFS 队列宽度)