695. 岛屿的最大面积 Medium
给你一个大小为 m x n 的二进制矩阵 grid 。
岛屿 是由一些相邻的 1 (代表土地) 构成的组合,这里的「相邻」要求两个 1 必须在 水平或者竖直的四个方向上 相邻。你可以假设 grid 的四个边缘都被 0(代表水)包围着。
岛屿的面积是岛上值为 1 的单元格的数目。
计算并返回 grid 中最大的岛屿面积。如果没有岛屿,则返回面积为 0 。
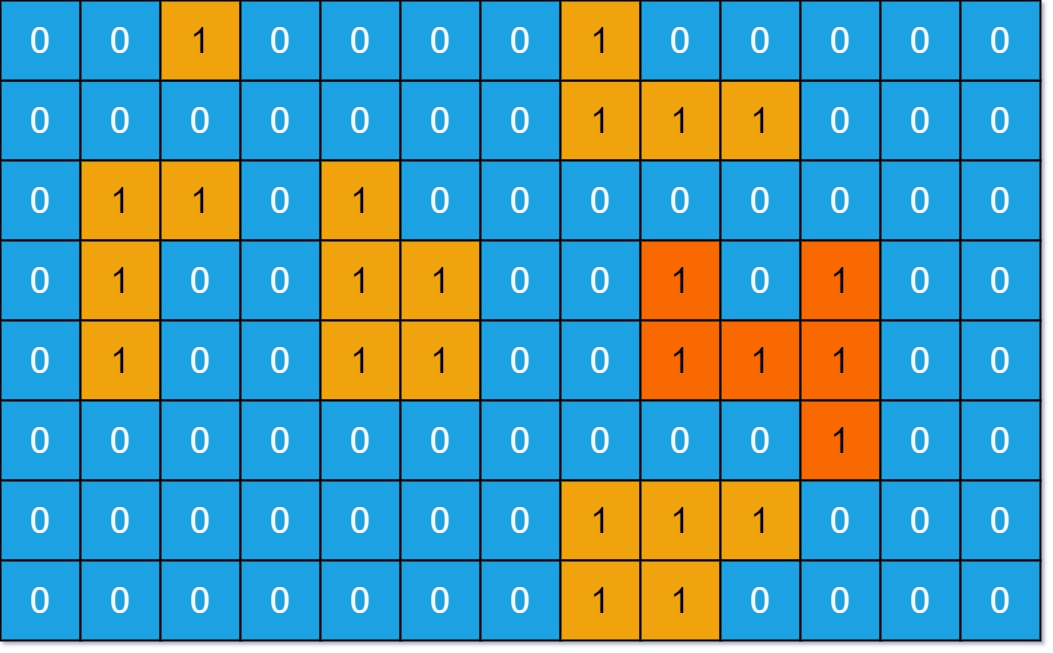
示例 1:
输入:grid = [
[0,0,1,0,0,0,0,1,0,0,0,0,0],
[0,0,0,0,0,0,0,1,1,1,0,0,0],
[0,1,1,0,1,0,0,0,0,0,0,0,0],
[0,1,0,0,1,1,0,0,1,0,1,0,0],
[0,1,0,0,1,1,0,0,1,1,1,0,0],
[0,0,0,0,0,0,0,0,0,0,1,0,0],
[0,0,0,0,0,0,0,1,1,1,0,0,0],
[0,0,0,0,0,0,0,1,1,0,0,0,0]
]
输出:6
解释:答案不应该是 11 ,因为岛屿只能包含水平或垂直这四个方向上的 1 。
示例 2:
输入:grid = [[0,0,0,0,0,0,0,0]]
输出:0
解题思路
输入: 一个由 1(陆地)和 0(水)组成的的二维网格
输出: 计算岛屿的最大面积
本题属于网格图 DFS 类问题。
这道题和 200.岛屿数量 解法类似
我们依然是通过 dfs 遍历将一块陆地的边界探索出来,当我们探索到边界外或者遇到已经遍历过的岛屿,此时不应该计算面积所以直接返回 0
其他情况都要将上下左右的面积累加起来并且加上自身的面积 1 dfs(r + 1, c) + dfs(r - 1, c) + dfs(r, c + 1) + dfs(r, c - 1) + 1
代码实现
class Solution:
def maxAreaOfIsland(self, grid: List[List[int]]) -> int:
rows, cols = len(grid), len(grid[0]) # 获取网格的行列数
# 定义 DFS 函数:用于计算从 (r, c) 出发的岛屿面积
def dfs(r, c):
# 如果越界,或者当前不是陆地(值为 0),直接返回面积 0
if r < 0 or r >= rows or c < 0 or c >= cols or grid[r][c] == 0:
return 0
grid[r][c] = 0 # 将当前格子标记为已访问(淹掉陆地)
# 向四个方向扩展,累加相邻陆地的面积
area = 1
area += dfs(r + 1, c) # 向下
area += dfs(r - 1, c) # 向上
area += dfs(r, c + 1) # 向右
area += dfs(r, c - 1) # 向左
return area
maxArea = 0 # 用于记录最大的岛屿面积
# 遍历整个网格
for r in range(rows):
for c in range(cols):
if grid[r][c] == 1: # 如果是陆地
# 计算当前岛屿的面积,并尝试更新最大值
maxArea = max(maxArea, dfs(r, c))
return maxArea/**
* @param {number[][]} grid
* @return {number}
*/
var maxAreaOfIsland = function(grid) {
const rows = grid.length;
const cols = grid[0].length;
function dfs(r, c) {
if (r < 0 || r >= rows || c < 0 || c >= cols || grid[r][c] == 0) {
return 0;
}
grid[r][c] = 0;
let area = 0;
area += dfs(r + 1, c);
area += dfs(r - 1, c);
area += dfs(r, c + 1);
area += dfs(r, c - 1);
return area + 1;
}
let maxArea = 0;
for (let r = 0; r < rows; r++) {
for (let c = 0; c < cols; c++) {
maxArea = Math.max(maxArea, dfs(r, c));
}
}
return maxArea;
};复杂度分析
时间复杂度:O(m * n)
空间复杂度:O(m * n)