437. 路径总和 III Medium

给定一个二叉树的根节点 root ，和一个整数 targetSum ，求该二叉树里节点值之和等于 targetSum 的 路径 的数目。

路径 不需要从根节点开始，也不需要在叶子节点结束，但是路径方向必须是向下的（只能从父节点到子节点）。

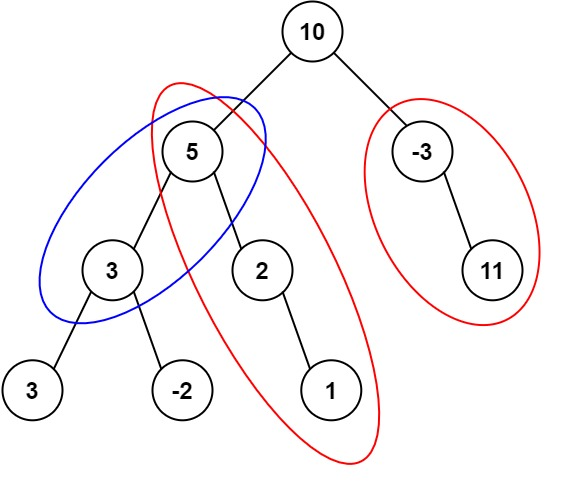
示例 1:
输入：root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出：3
解释：和等于 8 的路径有 3 条，如图所示。

示例 2:
输入：root = [5,4,8,11,null,13,4,7,2,null,null,5,1], targetSum = 22
输出：3

解题思路

输入：二叉树的根节点 root，一个整数 targetSum

输出：返回该二叉树里节点值之和等于 targetSum 的 路径 的数目

本题适合使用自顶向下 DFS + 前缀和 + 哈希 解决。

• DFS 前序遍历，维护当前前缀和 curr。
• 用哈希表 cnt 记录“某个前缀和出现的次数”。初始化 cnt[0] = 1（空路径前缀）。
• 对每个节点：
  1. curr += node.val
  2. 将 cnt[curr - targetSum] 计入答案（这些就是以当前节点为终点的合法路径条数）
  3. cnt[curr]++
  4. 递归左右子树
  5. 回溯：cnt[curr]--（返回父节点前把当前贡献撤回）

代码实现

python

class Solution:
    def pathSum(self, root: Optional[TreeNode], targetSum: int) -> int:
        # 使用字典记录前缀和及其出现次数，sums[total] 表示前缀和为 total 的路径数
        sums = defaultdict(int)
        sums[0] = 1  # 初始化，表示从根节点开始就有一个前缀和为 0 的路径
        
        # 深度优先搜索，total 表示当前路径的总和
        def dfs(root, total):
            count = 0
            if root:  # 递归结束条件：当前节点为空时返回 0
                # 更新当前路径和
                total += root.val

                # 如果存在前缀和为 total - targetSum 的路径，说明找到了一条和为 targetSum 的路径
                count = sums[total - targetSum]

                # 将当前路径和加入 sums 中，表示当前路径和出现了一次
                sums[total] += 1
                
                # 递归计算左子树和右子树中的路径和
                count += dfs(root.left, total) + dfs(root.right, total)
                
                # 回溯：遍历完当前节点的左右子树后，移除当前路径和的记录，避免影响其他路径的计算
                sums[total] -= 1
            return count
        
        # 从根节点开始，初始路径和为 0
        return dfs(root, 0)

javascript

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @param {number} targetSum
 * @return {number}
 */
var pathSum = function (root, targetSum) {
    const cnt = new Map();
    cnt.set(0, 1); // 空前缀

    const dfs = (node, curr) => {
        if (!node) return 0;

        curr += node.val;
        // 以当前节点为终点、和为 target 的路径数量
        const need = curr - targetSum;
        let res = cnt.get(need) || 0;

        // 进入子树前记录当前前缀和
        cnt.set(curr, (cnt.get(curr) || 0) + 1);
        res += dfs(node.left, curr);
        res += dfs(node.right, curr);
        // 回溯
        cnt.set(curr, cnt.get(curr) - 1);

        return res;
    };

    return dfs(root, 0);
};

复杂度分析

时间复杂度：O(n)

空间复杂度：O(h)

链接

437 国际版

437 中文版