11. 盛最多水的容器 Medium

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

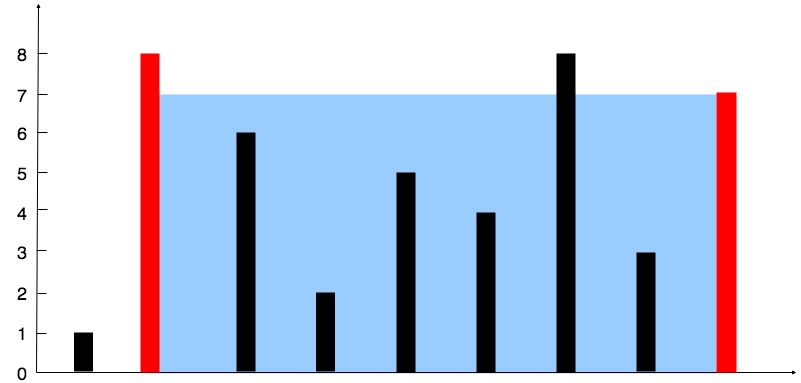
示例 1：
输入：[1,8,6,2,5,4,8,3,7]
输出：49
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：
输入：height = [1,1]
输出：1

解题思路

输入：一个整数数组 height

输出：找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

本题是典型的 相向双指针 问题。

核心逻辑

每次选择两根线构成容器，装水的容量由两条线中较短的一条决定：

• 高度：min(height[left], height[right])
• 宽度：right - left
• 面积（容量）：area = height * width

移动策略

每次比较两端的高度：

• 谁更矮，谁往中间移动（试图找到更高的线）
• 因为更短的一方限制了水的高度，只有换掉它，才可能得到更大的面积

算法流程

1. 初始化左右指针 left = 0, right = n - 1

2. 循环直到两指针相遇：

   • 计算当前面积并更新最大值
   • 移动较短边的指针

3. 返回最大面积

代码实现

python

class Solution:
    def maxArea(self, height: List[int]) -> int:
        # 初始化左右指针
        left, right = 0, len(height) - 1
        max_area = 0  # 用于记录最大容量

        # 双指针向中间移动
        while left < right:
            # 计算当前左右指针对应的面积
            width = right - left
            h = min(height[left], height[right])
            area = width * h
            max_area = max(max_area, area)

            # 谁的高度更小，就移动谁（因为移动更高的一方只会变小）
            if height[left] < height[right]:
                left += 1
            else:
                right -= 1

        return max_area

javascript

/**
 * @param {number[]} height
 * @return {number}
 */
var maxArea = function(height) {
    let left = 0;
    let right = height.length - 1;
    let maxArea = 0;

    while (left < right) {
        const h = Math.min(height[left], height[right]);
        const w = right - left;

        const area = w * h;
        maxArea = Math.max(maxArea, area);

        if (height[left] < height[right]) {
            left ++;
        } else {
            right --;
        }
    }
    
    return maxArea;
};

复杂度分析

时间复杂度：O(n)

空间复杂度：O(1)

链接

11 国际版

11 中文版